多項式の基本1|「展開」と「因数分解」の4つの基本公式 15/9/24 21/2/15 多項式 小学校までの「算数」と中学校からの「数学」との大きな違いの1つとして, 「文字」を使うか使わないかということが挙げられます.¶エルミート多項式. 次の関係式: φ(x)hj(x) = (−1)j dj dxj φ(x) を満たす多項式hj(x)をエルミート多項式という. µ コーニッシュ・フィッシャー展開 冒頭の仮説検定問題では%点を求める必要がある.最後にこの求め方に触れる.wα をSn の上側α%点,zα を標準正規分布の上側α%点とする.この多項式環を生成するには,三通りのやり方がある. sage R = PolynomialRing(QQ, 't') sage R Univariate Polynomial Ring in t over Rational Field このやり方では,多項式環を生成し,画面表示時の変数名として (文字列) t を割り当てている. ただし,これはSage内で使うために

多項式の乗法の公式 数学i フリー教材開発コミュニティ Ftext
多項式の展開とは
多項式の展開とは-2x2-3x+4 のように、単項式の和や積で表される式を 多項式 といいます。 多項式では、ひとつひとつの単項式のことを 項 といい、文字を含まない数字だけの項を 定数項 といいます。ベキ関数の和によっていろいろな関数を作ることができます。 これを自在に作るためにはどうしたら良いのでしょうか? 今度は、ある関数は無限のベキ関数の級数に表すことができるとしましょう。 そうすると、微分をすることで、それぞれの係数を求めることができます。




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
ラゲール多項式の諸性質と証明 ラゲール多項式 はラゲールの微分方程式を満たすである。 母関数 母関数は となる。 多項式展開 母関数を使って のように多項式展開できる。ここで、 についての和は の代わりに でも良い。なぜなら で上記の式は3次の多項式ならば成立する式であり、 を含む開区間で が微分可能なとき次のようなことが言えます。 以上をテイラー展開と呼び、 式の での値を まわりで展開するといったりします。 ちなみに分母にある というのは、nのカイジョウとよび、以下のように定義されているものです。2変数関数 \ (f (x,\ y)\) について,2次のテイラー多項式を求めます。 微分とは何であるか? という問いにザックリと答えますと 1変数関数であれば,ある点(例えば \ (x_0\) )の近くでの \ (f (x)\) の値を接線の式で近似すること 2変数関数であれば,ある点
All text is available under the terms of the GNU Free Documentation License この記事は、ウィキペディアの多項式の展開 (改訂履歴)の記事を複製、再配布したものにあたり、GNU Free Documentation Licenseというライセンスの下で提供されています。 Weblio辞書に掲載されているウィキペディアの記事も、全てGNU Freeテイラー多項式・マクローリン多項式 関数 \(f(x)\) の1次近似式を作るためには,導関数 \(f'(x)\) が存在しなければなりません。 さらに,2次近似式を作るためには,2次導関数 \(f''(x)\) が存在しなければなりません。 それでは,関数 \(f(x)\) が3階,4階と微分可能であれば, \(f(x)\) を3次や4次の展開公式を丸ごと覚えるのではなく,導けるようにしましょう。 19 19 19 も同様に式の対称性と多項定理から一瞬で導けます。 このように対称式の展開は「対称性,多項定理,係数の和」に注目 して瞬時に行えるようになっておくのが理想です。
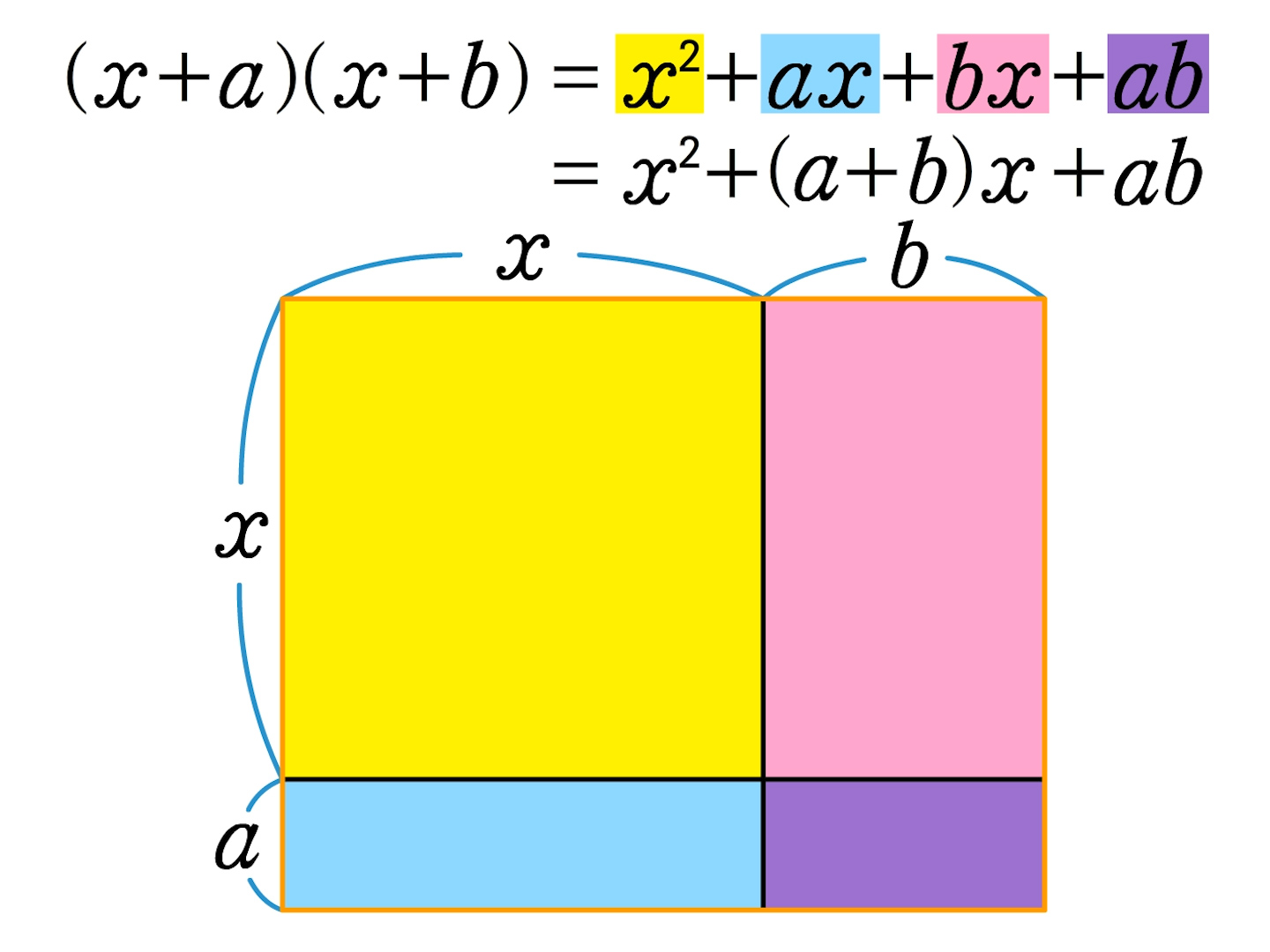
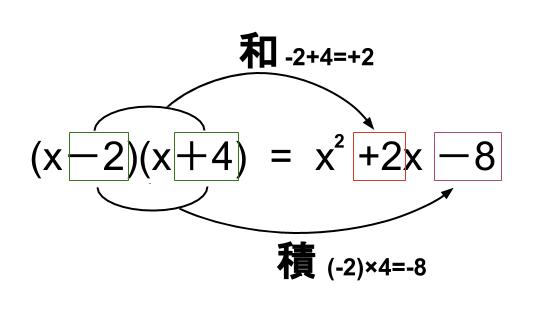
次は同じ多項式同士が掛けられている場合、すなわち、2乗となっている場合にこのように展開できるという公式です。 この式の左辺は と書くことが出来ますが、これは1つ目の公式 の が に変わっただけ 〜今回のテーマ〜 多項式の分配法則や乗法の公式等、展開のやり方を覚えよう。 その他の単元や計算問題はこちら ↓ ↓ ↓ はじめに このシリーズでは、各教科・各単元に登場する基本事項(用語やその定義、公式等)を中心にまとめていきます。 現役中学生・高校生の軽い予習・復習多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後



3年 図形で考えよう X A X B 数学イメージ動画集 大日本図書




中学3年 数学の世界3 多項式の計算と式の展開 教科書予習復習練習問題 赤城 ᐡᐤᐡ
単項式も多項式の一つの場合に過ぎないという見方でとらえられている。 このページでは、(1+x) n の展開について考える。 この多項式の展開については、当HPの「パスカルの三角形」で既に述べらCode Revisions 5 1変数多項式の展開プログラム(いろんなサンプルコードつき) Raw expansionrb # 1変数多項式の展開プログラム class Polynomial @@DEFAULT_MAX_ORDER = 0 @@max_order = @@DEFAULT_MAX_ORDER # 打ち切らずに計算させる最大の次数 ( (MAX_ORDER1) 以上の次数は打ち切らこのルジャンドル多項式を用いた展開は、例えば連続質量や電荷分布の上でこの展開を積分するときなどに有用である。 ルジャンドル多項式は、空間の無電荷領域における 電位 に関する ラプラス方程式 ∇ 2 Φ ( x ) = 0 {\displaystyle \nabla ^ {2}\Phi ( {\boldsymbol {x
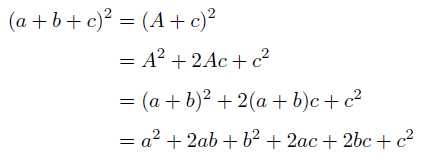



置き換えによる式の展開 まなびの学園



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su
通常,式の展開は次のような順序で,「総当たりで」掛けると考えることが多いが,二項定理,多項定理の解説はこの方法では分かりにくいので,「代表選手の選び方」で解説してみる. 右図のように各々の( )からどちらか1つの項 a , b を選んで 多重極展開の一般項を求めてみよう. これはすぐにわかって,上で現れたTaylor展開がLegendre多項式 の母函数になっていることから, である. ここでLegendreの多項式は, で表される直交多項式である( は床函数で を超えない最大の整数を表す). Problems関数のチェビシェフ級数展開による数値積分法 – コーシーの主値積分– 01mm081 清水香織 指導教員 鳥居達生 1 はじめに 本研究では, まずチェビシェフ多項式の性質について 学び,これをもとに関数のチェビシェフ級数展開その項 別積分およびコーシーの主値積分の計算法について述べ



高校入試 英語 数学 多項式 式の展開



Studydoctor分配法則による多項式の展開 中3数学 Studydoctor
式のカッコをはずすことを 「式を展開 (てんかい)する」 と言います。多項式に関することだし、微分方程式のページに入れるかどうか迷ったけれど、ルジャンドル多項式が微分方程式で大事な関数だからここに入れることにした。 1ポテンシャルの近似展開 として、この関数\(f(x)\)について\(x=0\)のまわりの展開式を求めてについて、やり方をイチから確認していきます。 挑戦していく問題はこちら! 次の展開式において、 内に指定された項の係数を求めよ。 二項定理を確認! (2)の解説、約分ができるので注意! 定数項は? (4)の解説、同じ文字がある場合は
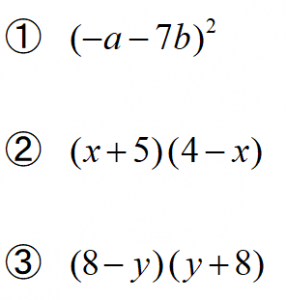



いろいろな多項式を展開してみよう 前編 インターネット家庭教師のアスミラ



U9j580gf8iba369ji2w Xyz P 565
多項式の基本6|3次以上の展開と因数分解の公式の総まとめ 前々回の記事で説明したように,たとえば x 2 − 2 x − 2 = 0 のような簡単には因数分解できない2次方程式は,いったん解を求めることによって因数分解できるのでした. では,3次式では因数分解1 10x2 19xy6y2 6x2 xy2y2 2a2 15ab28b2 18a2 3ab10b2 32x2 12xy9y2 4x2 4xy63y2 2 a2 ab2ab1 x2 2xyy2 2x2y a2 abac2a2b2c a2 3ab2b2 3a6b 2x2 5xy3y2 8x12y 3a2 5ab2b2 3acbc 3 a2 3ab2b2 4a5b3 x2 y2 x3y2 中学校英語学習サイト 中学英語の文法、練習問題、リスニング 中学校About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators
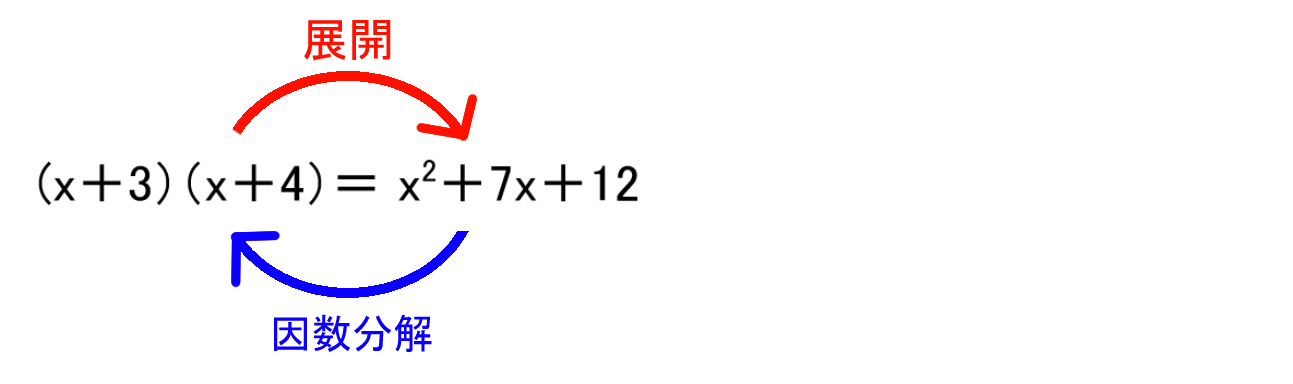



多項式 2 展開と因数分解 バカでもわかる 中学数学




多項式の展開公式の説明 おかわりドリル
つまり, マクローリン展開を用いると,一般の関数 f (x) f (x) を多項式で近似することができる。2)「実行」-「各種の展開」-「多項式展開」を選びます。 3)展開する最高次数の入力になりますので、11と入力し、「OK」をクリックします。 4)関数の代数計算の形で表示されます。 taylor_expand( sinx ,11) =12x 2 1 x 24 1 x 60 1 x 7 1 x 403 1 x 1 x1 xy2xy2 ab3a2b6 ax3a4x12 axax1 4xy2x2y1 8ab4a2b1 6ab4a9b6 2xy4xy2 2 ac2bca2b ax4ay2x8y 6x2 8xy3x4y 12x2 54xy10x45y axbxayby 2axbx6ay3by 8a2 12ab2ac3bc 10xy2y2 15xz3yz 中学校英語学習サイト 中学英語の文法、練習問題、リスニング 中学校数学学習サイト 中学




多項式の乗法の公式 数学i フリー教材開発コミュニティ Ftext




中学数学 多項式 の教え方 展開の応用問題
多項式の展開 多項式の展開の概要 ナビゲーションに移動検索に移動目次1 概要2 具体例3 冪級数への拡張31 例4 関連項目5面積と式の展開 このシミュレーションの実行可能なコピーを組み込むためには、このHTMLコードをお使いください。 HTMLコード内の"width"と"height"の属性を変更することによって、組み込まれたシミュレーションの幅と高さを調整できます。 「クリックしてまずは"項に区切る""分配する"から「式の展開」を始めましょう。 (1) 単項式×多項式を展開する 例えば,2 ( a +3 ) の展開を考えてみ




多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後




中3 中3 式の展開 中学生 数学のノート Clear
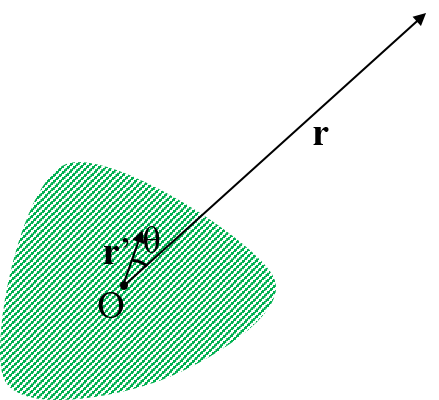



ポテンシャルの近似展開とルジャンドル多項式 物理とか




式の展開 多項式と多項式の掛け算 中学数学 By じょばんに マナペディア




バカでもわかる 中学数学 多項式 展開 因数分解など
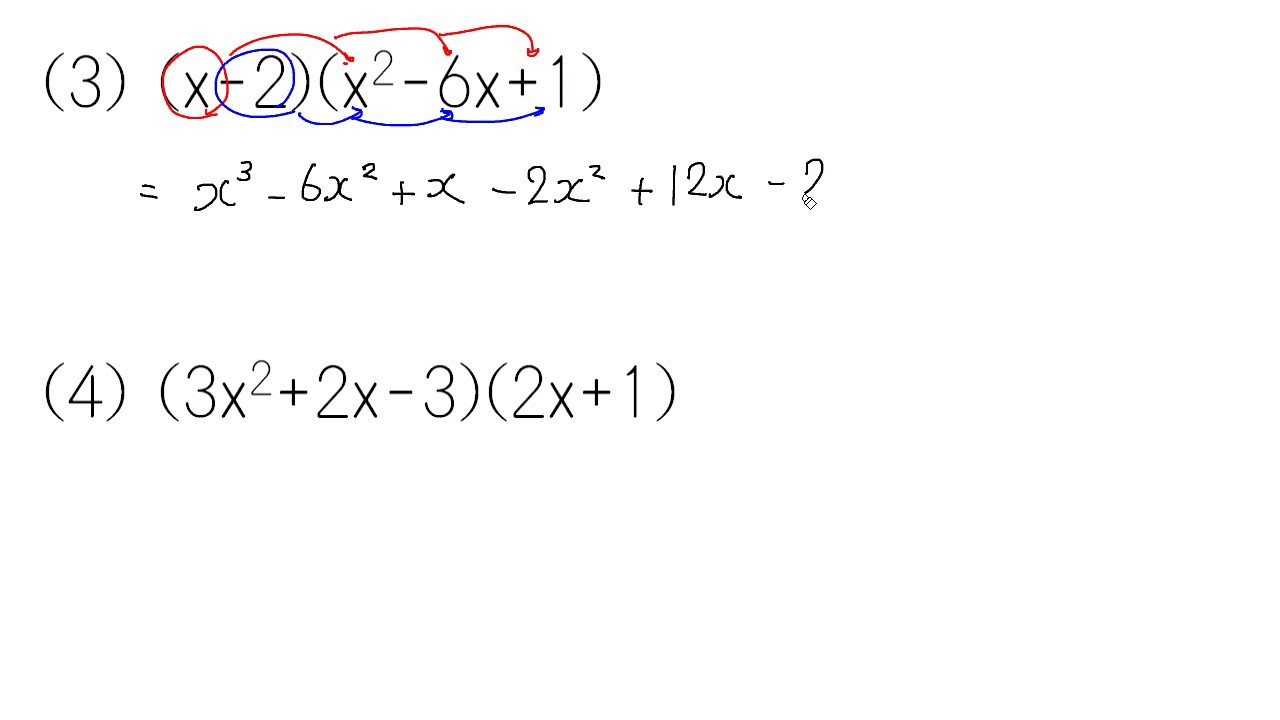



多項式の展開 Youtube




テイラー展開 マクローリン展開 理系ノート



Www Nhk Or Jp Kokokoza Library Tv Basicmath Archive Basic Suu 12 Pdf
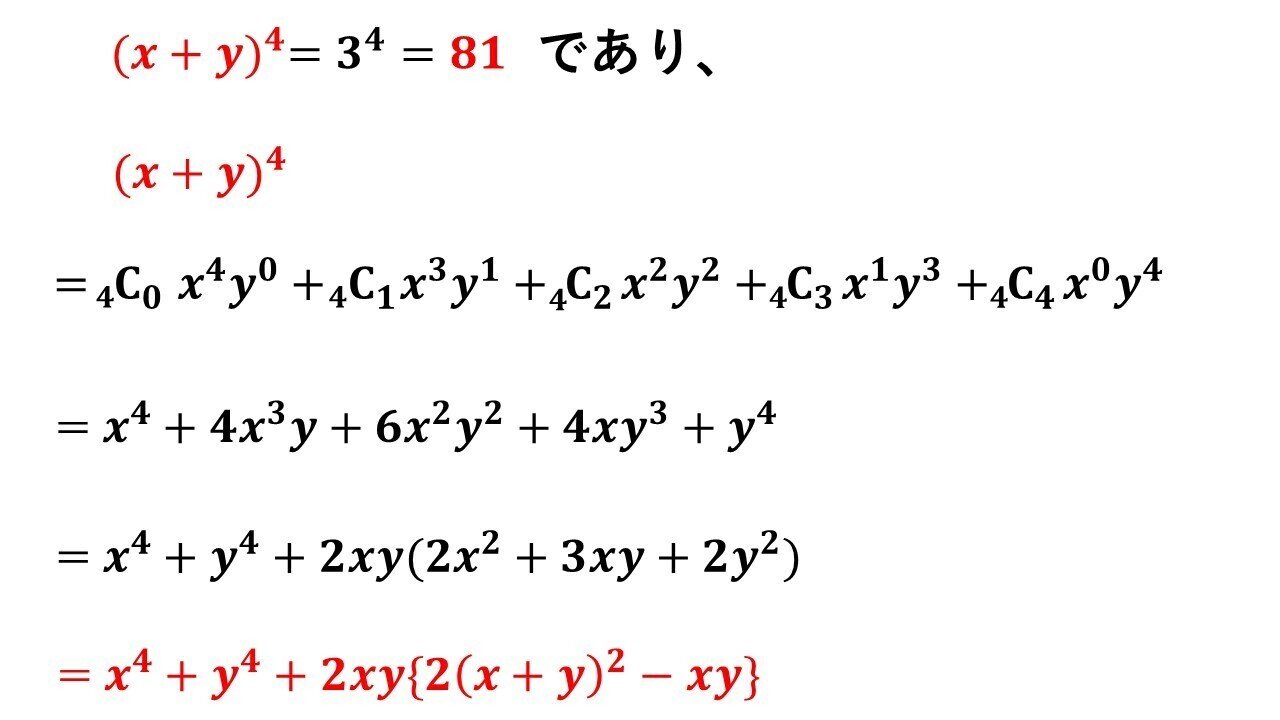



基本対称式の計算問題と二項展開 タロウ岩井の数学と英語 Note



1



1



展開公式



1 1 式の展開 乗法公式の利用 テスティー




中3 展開と因数分解3 多項式と単項式のいろいろな計算 予習 中学数学の勉強に
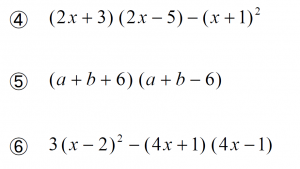



いろいろな多項式を展開してみよう 後編 インターネット家庭教師のアスミラ



3 8第1章多項式 乗法公式 いろいろな式の展開 中学生




中学数学 多項式の計算 ママ塾ノート




中学数学 式の展開 因数分解




中3 数学 式の展開 授業ノート 中学生 数学のノート Clear




展開 と 因数分解 の4つの基本公式



数学 展開 公式 数学の展開問題 解き方のコツ 公式 スタディサプリ大学受験講座 Www Ourfuture Qld Gov Au
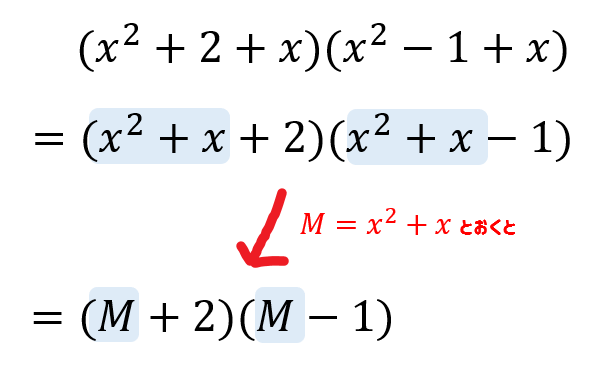



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん
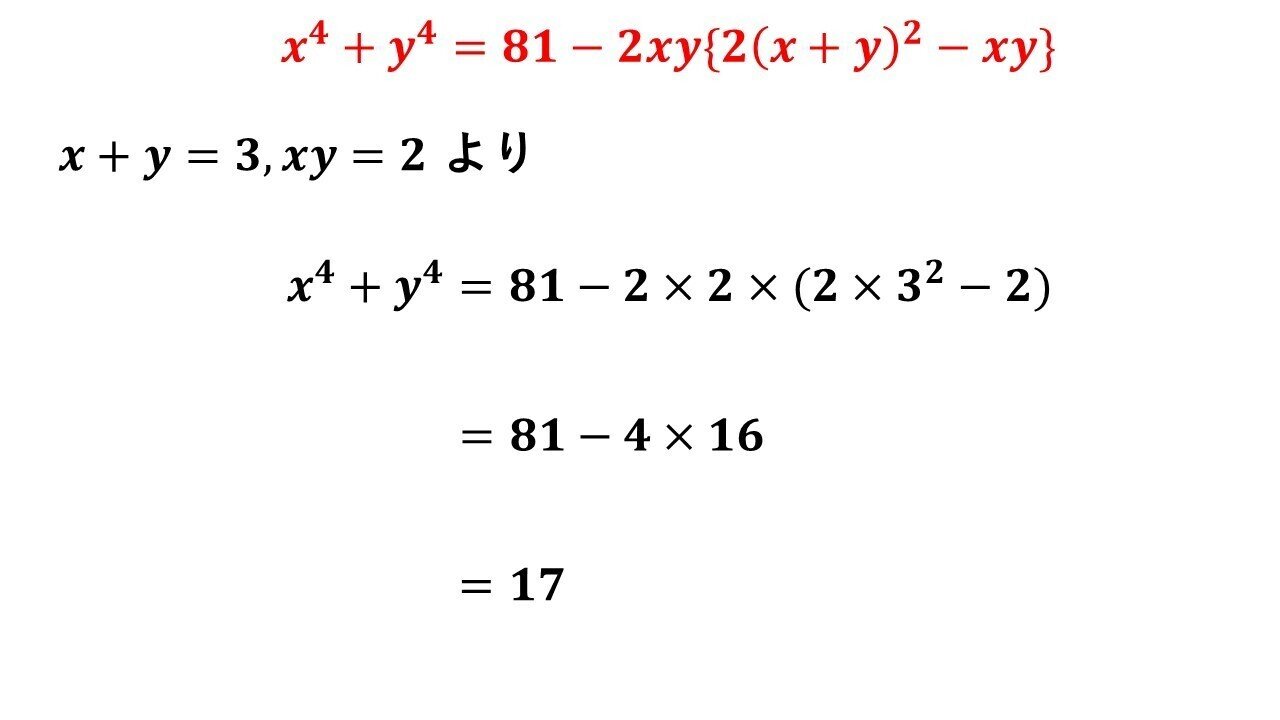



基本対称式の計算問題と二項展開 タロウ岩井の数学と英語 Note



2




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん
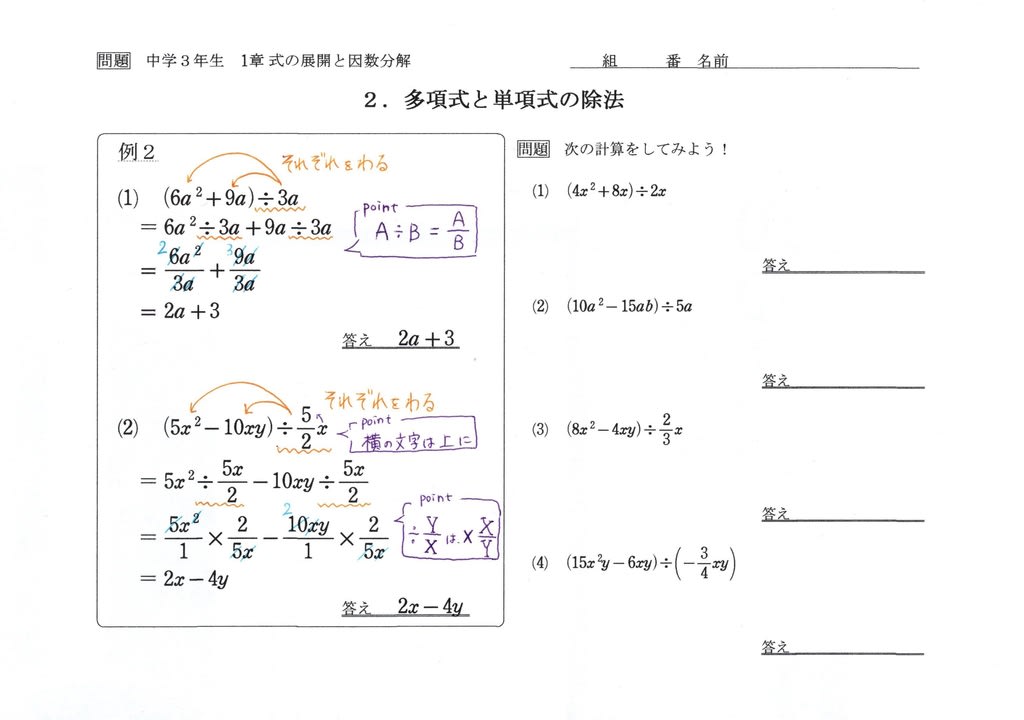



中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に




中学数学 多項式 の教え方 展開の基本



こんにちは 数学の 多項式の展開 で質問があります わからない問題 Yahoo 知恵袋




多項式の展開図解 Geogebra




4 5 いまさらきけない多項式 展開の練習 理一の数学事始め Note




式の展開と因数分解 の問題のわからないを5分で解決 映像授業のtry It トライイット




テイラーの定理とその証明 おいしい数学
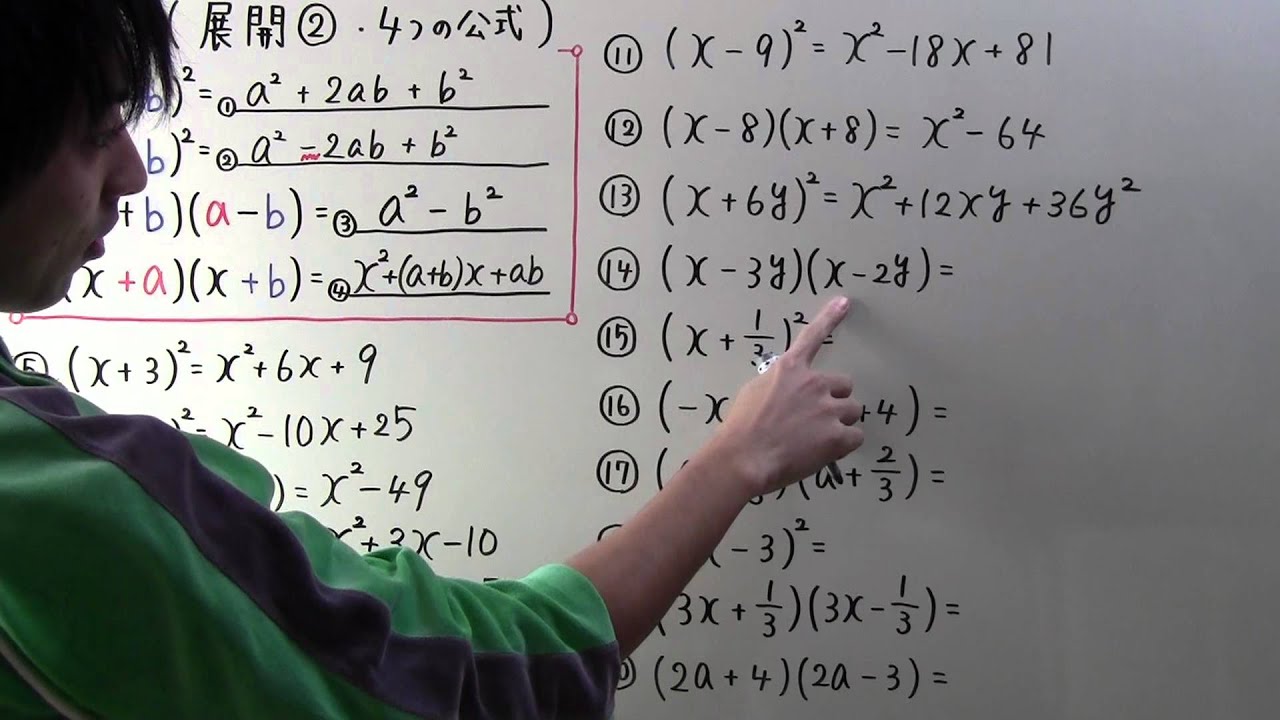



数学 中3 3 展開 4つの公式 Youtube




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




2 1熱身q7 展開多項式 中二數學 Youtube




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




数学 展開 公式 数学の展開問題 解き方のコツ 公式 スタディサプリ大学受験講座 Www Ourfuture Qld Gov Au




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく




高校数学 多項定理 A B C Nの展開式の係数 受験の月




3次以上の展開と因数分解はどうなる 公式の総まとめ




多項式の掛け算 展開 を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
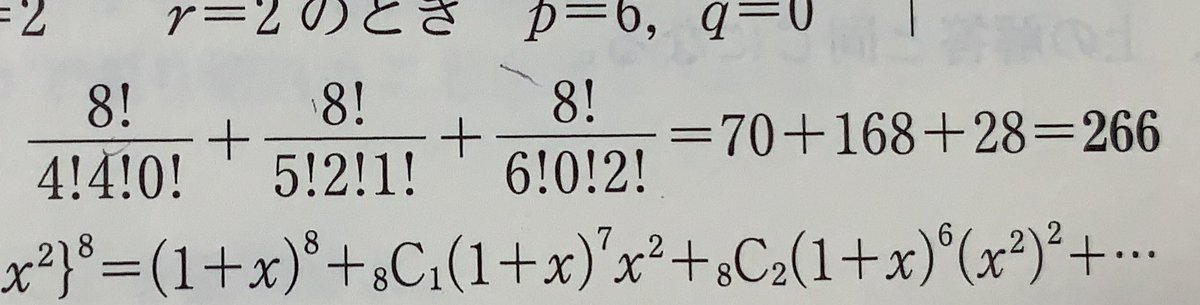



多項式




多項式の乗法公式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに
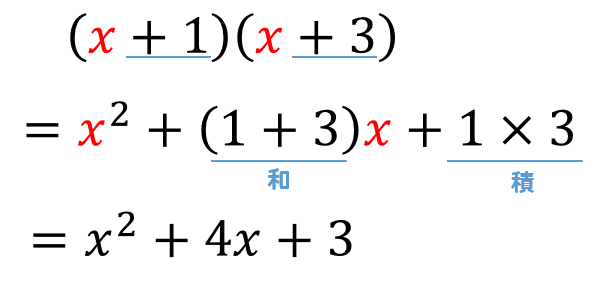



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ




バカでもわかる 中学数学 多項式 展開 因数分解など




中学3年数学 式の展開と因数分解 多項式の計算 練習問題9 あんのん塾




多項式の乗法について 数学i フリー教材開発コミュニティ Ftext




中学3年数学 3項式の展開 Youtube
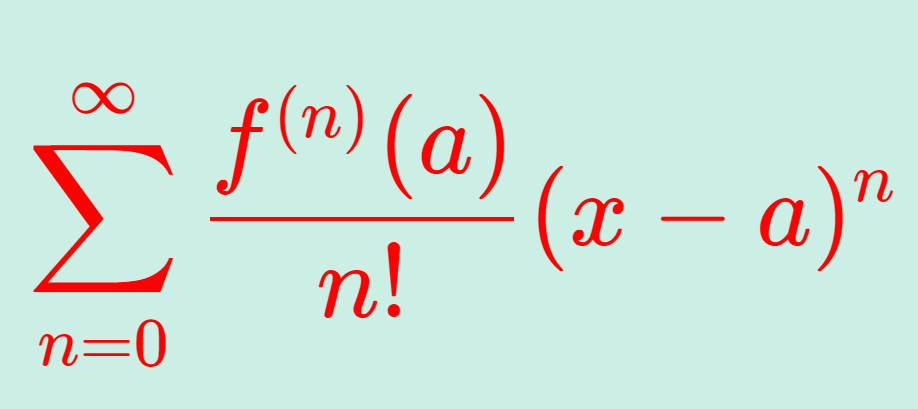



テイラー展開 マクローリン展開とは 解析的な関数と具体例 数学の景色




多項式の計算 解説 清水塾




多項式の乗法の公式 数学i フリー教材開発コミュニティ Ftext




中3 数学 多項式と単項式の乗除 式の展開 中学生 数学のノート Clear




式の展開の公式 多項式 多項式 中学数学 By じょばんに マナペディア




中学3年 数学の世界3 多項式の計算と式の展開 教科書予習復習練習問題 赤城 ᐡᐤᐡ




1994 号 関数近似計算方法 Astamuse




4つの乗法公式 教遊者




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学



多項式の積の展開についてです 答えを 7 2とするのが正解なの Yahoo 知恵袋
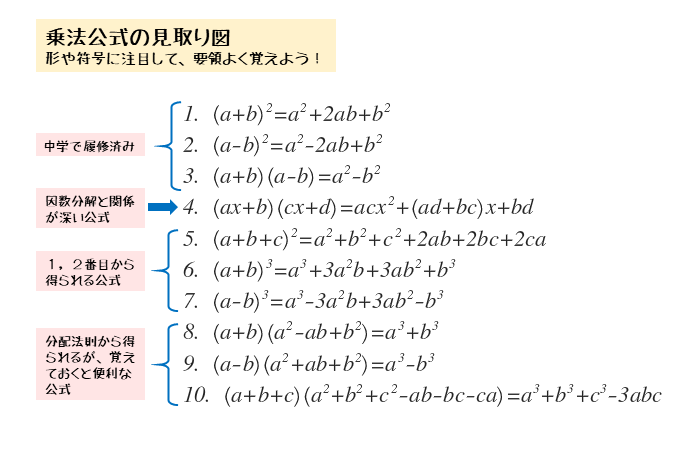



数と式 整式の展開に関する問題を解いてみよう 日々是鍛錬 ひびこれたんれん




多項式の乗法 本時の目標 展開の意味を理解し 分配法則を使って多項式の乗法の計算をすることができる Ppt Download




中学3年 Geomathroom




中学数学3年 単項式と多項式の乗法と除法 受験の月



Http Www Nyushi Sugaku Com Tyu3 T3 1 Y 01 Pdf



Studydoctor3項式の展開 中3数学 Studydoctor



Http Www Sagamihara Ohnominami J Ed Jp Pdf Suugaku Pdf
.jpg)



二項定理のしくみと意味 A B のn乗 高校数学なんちな
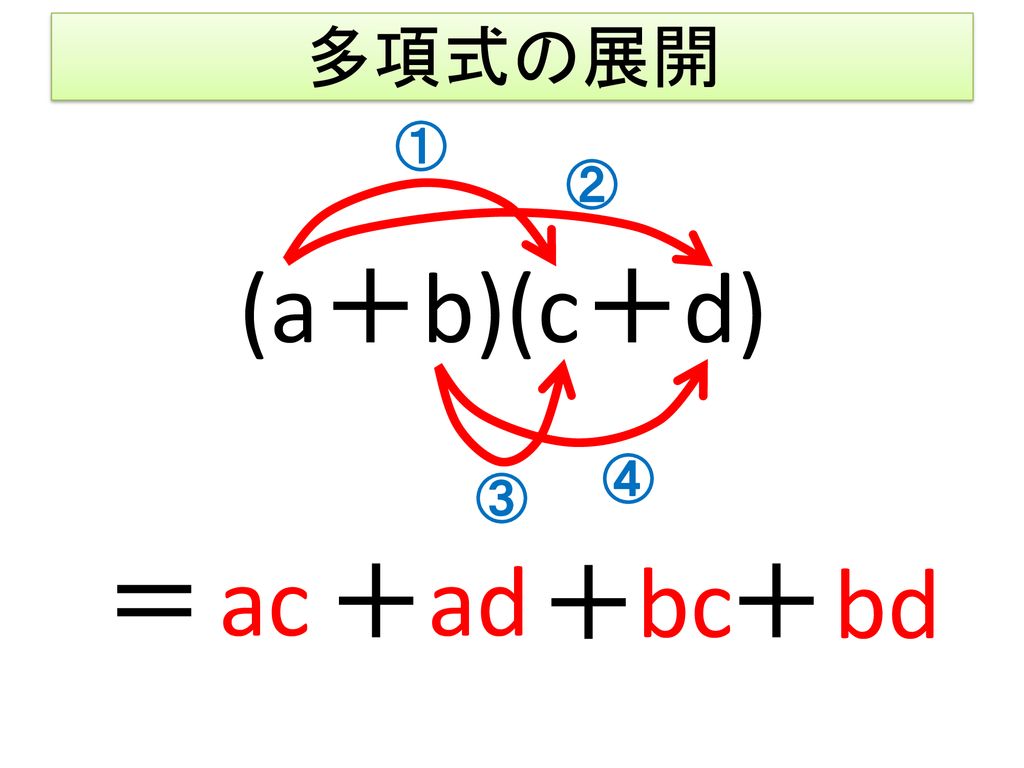



多項式の乗法 本時の目標 展開の意味を理解し 分配法則を使って多項式の乗法の計算をすることができる Ppt Download
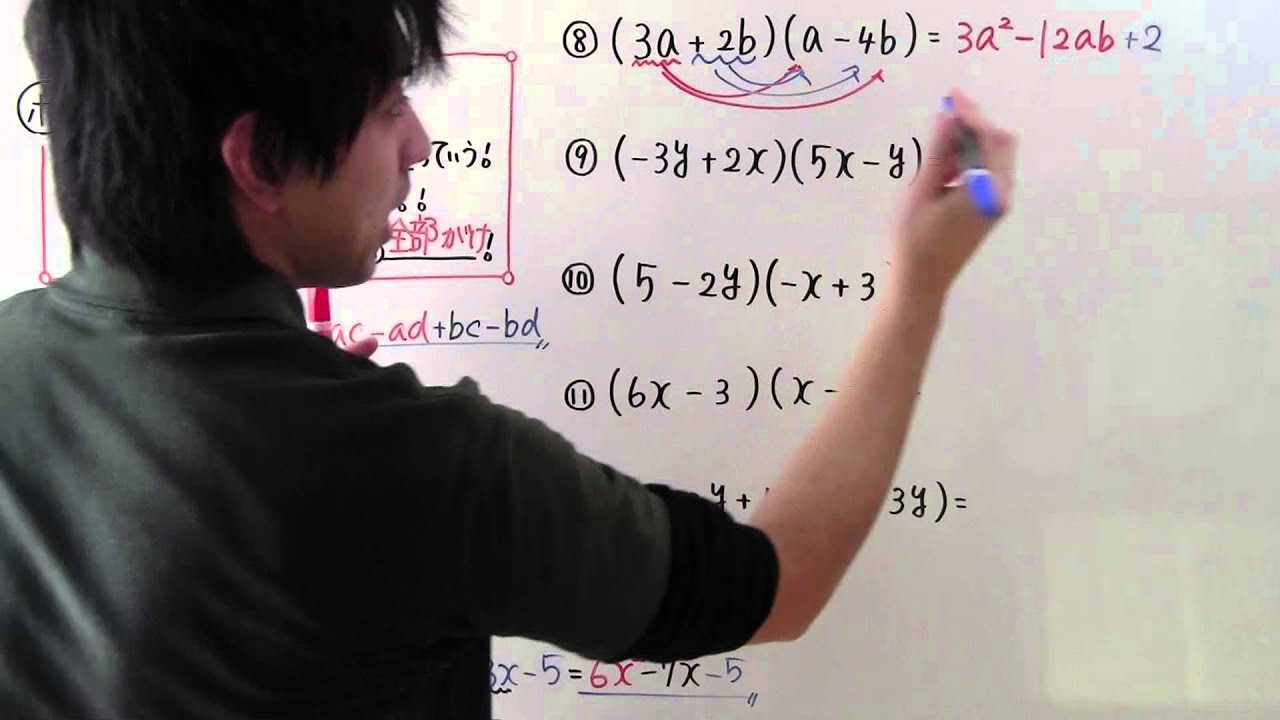



数学 中3 2 展開 Youtube



3 7第1章多項式 乗法公式 いろいろな式の展開




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学 式の展開の公式 やり方についてわかりやすく説明しました 都立高校受験応援ブログ




黒木玄 Gen Kuroki בטוויטר 整式 続き それを展開した結果ab Ad は 単項式 の和なので 多項式 になる そして記号の羅列に関してそのような操作をできることを等号 を使って表わすのだと説明しているようにも見える 算数教科書では等号が何を意味して




式のかけ算の筆算 数学の偏差値を上げて合格を目指す




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に




中3 展開と因数分解1 多項式と単項式の乗法 予習 中学数学の勉強に




中学数学 多項式と多項式の乗除 中学数学の無料オンライン学習サイトchu Su
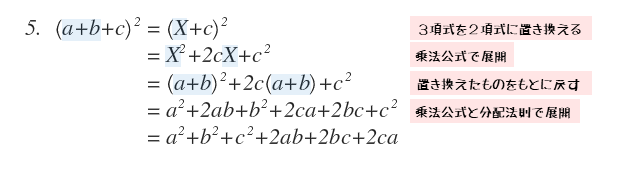



数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん
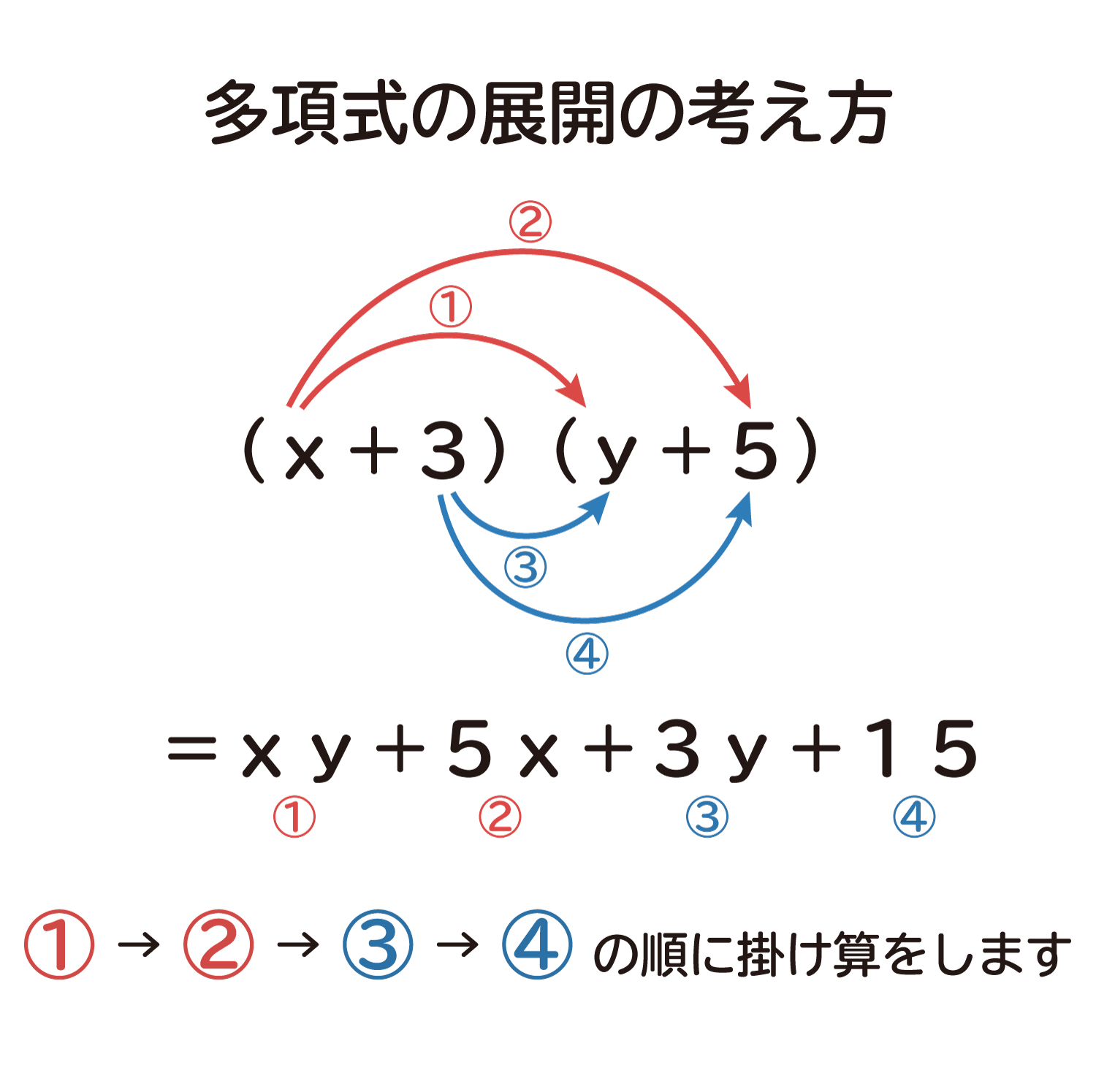



多項式同士の掛け算の展開の考え方 おかわりドリル
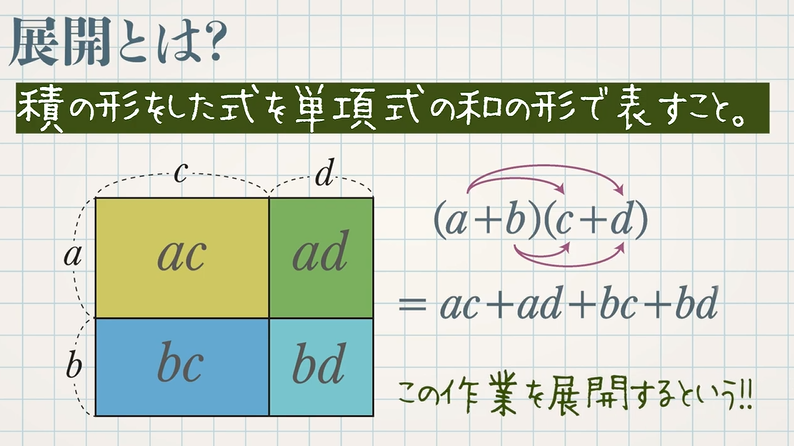



展開 多項式と多項式 教遊者




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




高校数学 展開のおさらい1 映像授業のtry It トライイット




中3 中3数学 式の計算 多項式の計算 乗法公式 式の展開 中学生 Clear



整式の乗法 多項式の展開公式 小テストno 3の解答 保谷高校数学科



1



中3数学 式の展開 多項式 短縮版 Mpg On Vimeo




マンツーマン授業の実況中継 富士宮教材開発 井出進学塾



多項式の乗法



2




中学数学 多項式の計算 ママ塾ノート



0 件のコメント:
コメントを投稿